Cutoff for random walk on random graphs with a community structure

Link to Join MS Teams Talk

This talk will be broadcast at 13:30 GMT 27th March on MS Teams only.

Meeting ID: 393 527 089 878
Passcode: dsm7py

Abstract

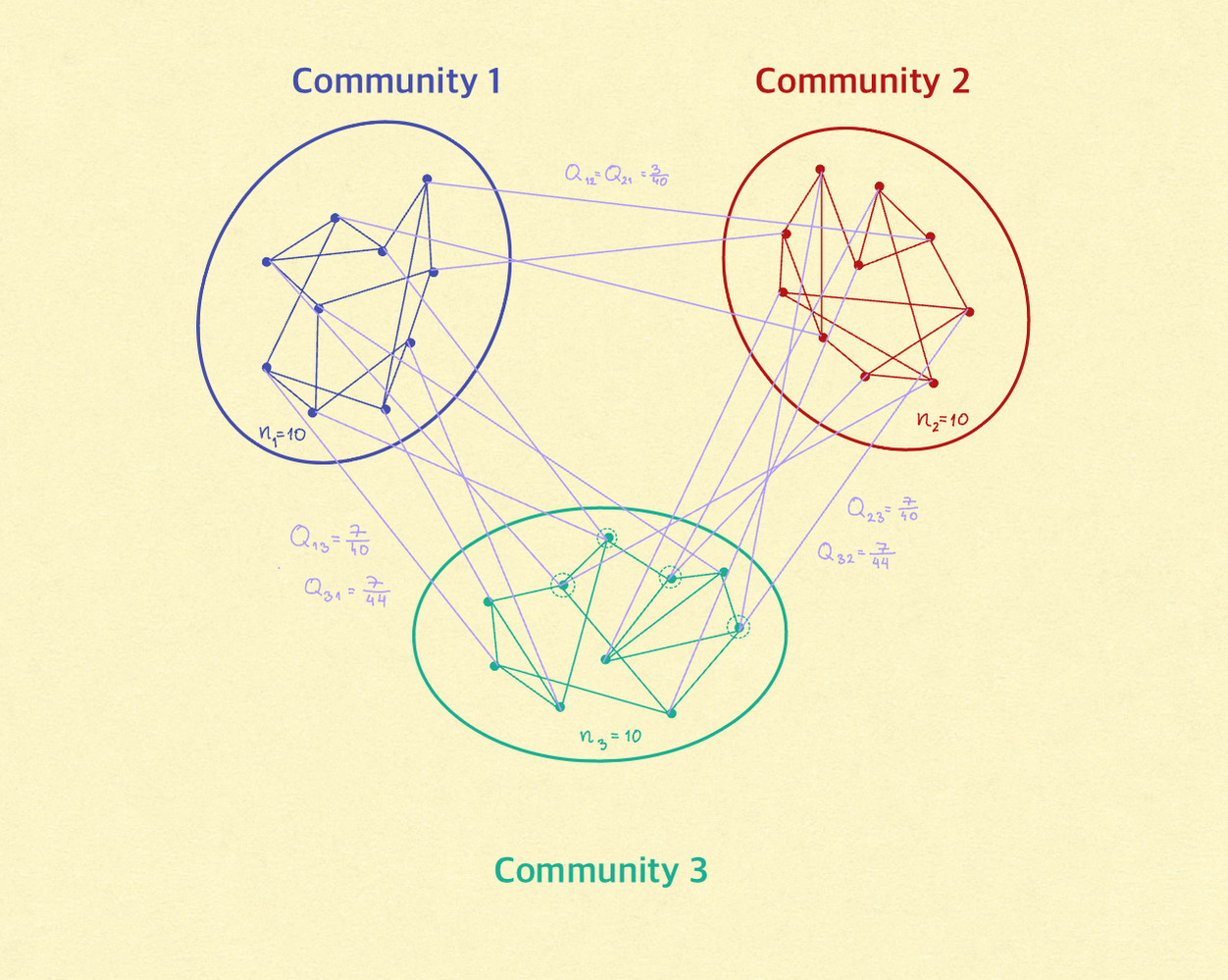
We consider a variant of the configuration model with an embedded community structure, where every vertex has an internal and an outgoing number of half edges. We pick a uniform matching of the half edges subject to the constraints that internal edges in each community are matched to each other and the proportion of half edges between communities $i$ and $j$ being $Q(i,j)$. We prove that a simple random walk on the resulting graph $G=(V,E)$ exhibits cutoff if and only if the product of the Cheeger constant of $Q$ times $\log|V|$ diverges. This is a joint work with Perla Sousi and Jonathan Hermon.

About Andjela

Andjela Sarkovic did her PhD with Perla Sousi on the topic of Mixing times of random walks on random graphs. She is currently a fellow and a college teaching officer at King’s College, Cambridge and continues to research this topic.